Comparison of common activation functions used in deep learning

Most used activation functions in deep learning

The activation function regulates when and with what intensity the neuron fires. These functions are essential for allowing the network to approximate non-linearities. In the case of not using a non-linear activation, the Multi-layer Perceptron would be nothing but a succession of linear operations that results in a linear function approximator.

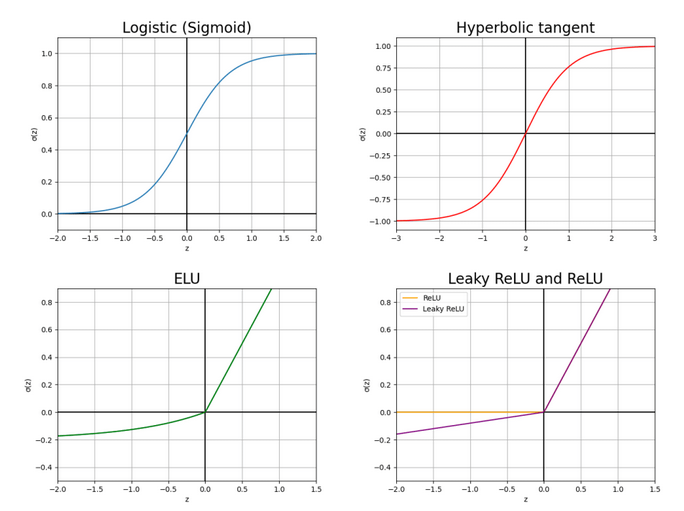
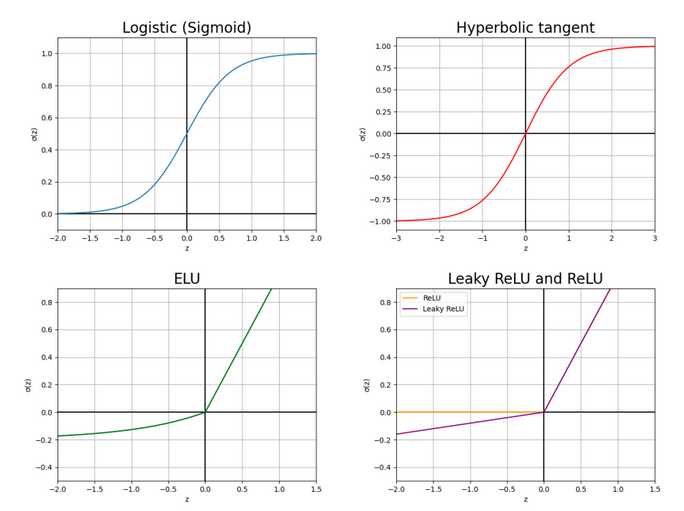
Comparison of common activation functions used in deep learning

Fig. 1 Different plots of the most relevant activation functions used in deep learning.

It is worth noting that the activation functions of the hidden layers and the one of the output layer can be different. Depending on the requirements of the network and the expected output, can be beneficial to use one function instead of another. This post goes through the activation functions explaining their pros and cons. Fig. 1 shows the graph for each of the activation functions listed below:

  • The family of Sigmoid functions are also used in logistic regression. Their mean is and they only return positive numbers since their outputs go in the range . They usually perform worse than the rest of the activation functions in this list as activation for the hidden layers 1. For this reason, they are usually used as activation of the output layer in the cases of binary classification or regression when the values are expected to be in the range .

(1)

  • The Hyperbolic tangent is a shifted and stretched version of the sigmoid function where the output values are in the range , having a mean for the outputs in zero. In most applications, it works better than the sigmoid function for the hidden layers since convergence is faster if the average of the input of each layer is close to zero, reducing the bias shift effect2.

(2)

  • The Rectified Linear Unit or ReLU3 is one of the most popular activations for DNNs. The derivative of the points of this function on the positive side is greater in comparison with the sigmoid and the hyperbolic tangent making the network learn faster in most cases. The simplicity of its derivative makes it computationally efficient and it is a non-saturating activation function preventing gradient vanishing, which is a problem when training the network as explained in this post.

(3)

  • The Leaky Rectified Linear Unit or Leaky ReLU4 is a type of activation function based on a ReLU, but it has a small slope for negative values instead of a flat slope. The slope coefficient is a hyperparameter that can be adjusted, with Eq. 4 exemplifying a value of . This activation function does not suffer from a ReLU problem known as “dying ReLUs”, where some neurons die out, meaning they keep on throwing 0 as outputs with the advancement in training. It also has the advantage of pushing mean unit activations closer to zero. In my modest personal experience, this activation function alongside the hyperbolic tangent, usually delivers the best performance.

(4)

  • The Exponential Linear Unit (ELU)5 is similar to the leaky ReLU. The difference is that the negative part is softened by a parameter as you can see in Eq. 5. ELUs saturate to a negative value with smaller inputs and thereby decrease the forward propagated variation and information.

(5)

Footnotes

  1. Nwankpa, Chigozie, et al. “Activation functions: Comparison of trends in practice and research for deep learning.” arXiv preprint arXiv:1811.03378 (2018). ↩

  2. LeCun, Y.A., Bottou, L., Orr, G.B., Müller, KR. (2012). Efficient BackProp. In: Montavon, G., Orr, G.B., Müller, KR. (eds) Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science, vol 7700. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-35289-8_3 ↩

  3. Glorot, X., Bordes, A. &; Bengio, Y.. (2011). Deep Sparse Rectifier Neural Networks. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, in Proceedings of Machine Learning Research 15:315-323 Available from https://proceedings.mlr.press/v15/glorot11a.html. ↩

  4. Maas, A. L., Hannun, A. Y., & Ng, A. Y. (2013, June). Rectifier nonlinearities improve neural network acoustic models. In Proc. icml (Vol. 30, No. 1, p. 3). (paper) ↩

  5. Clevert, D. A., Unterthiner, T., & Hochreiter, S. (2020). Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015. arXiv preprint arXiv:1511.07289. ↩